Signal Processing Basics¶

This chapter provides insights about several lock-in amplifier principles not necessarily linked to a specific instrument from Zurich Instruments. Since the appearance of the first valve-based lock-in amplifiers in the 1930s the physics have not changed, but the implementation and the performance have evolved greatly. Many good lock-in amplifier primers have appeared in the past decades, and some of them appear outdated now because they were written with analog instruments in mind. This section does not aim to replace any existing primer, but to complete them with a preferred emphasis on digital lock-in amplifiers.

The first subsection describes the principles of lock-in amplification, followed by the description of the function of discrete-time filters. After, we discuss the definition of the full range sensitivity, a specification parameter particularly important for analog lock-in amplifiers but with somewhat reduced importance for digital instruments. In the following, we describe the function and use of sinc filtering in particular for low-frequency lock-in measurements. The last section is dedicated to the zoom FFT feature. Innovative in the context of lock-in amplifiers, zoom FFT offers a fast and high-resolution spectral analysis around the lock-in operation frequency.

Principles of Lock-in Detection¶

Lock-in demodulation is a technique to measure the amplitude \(A_s\) and the phase \(\theta\) of a periodic signal with the frequency \(\omega_s = 2\pi f_s\) by comparing the signal to a reference signal. This technique is also called phase-sensitive detection. By averaging over time the signal-to-noise ratio (SNR) of a signal can be increased by orders of magnitude, allowing very small signals to be detected with a high accuracy making the lock-in amplifier a tool often used for signal recovery. For both signal recovery and phase-sensitive detection, the signal of interest is isolated with narrow band-pass filtering therefore reducing the impact of noise in the measured signal.

Figure 1 shows a basic measurement setup: a reference \(V_r\) signal is fed to the device under test. This reference signal is modified by the generally non-linear device with attenuation, amplification, phase shifting, and distortion, resulting in a signal \(V_s = A_s cos(\omega_s t + \theta_s)\) plus harmonic components.

Figure 1: Basic measurement setup incorporating a lock-in amplifier

For practical reasons, most lock-in amplifiers implement the band-pass filter with a mixer and a low-pass filter (depicted in Figure 2): the mixer shifts the signal of interest into the baseband, ideally to DC, and the low-pass filter cuts all unwanted higher frequencies.

Figure 2: Mixing and low-pass filtering performed by the lock-in amplifier

The input signal \(V_s(t)\) is multiplied by the reference signal \(V_r(t) = \sqrt{2}e^{-i\omega_r t}\) , where \(\omega_r = 2\pi f_r\) is the demodulation frequency and i is the imaginary unit. This is the complex representation of a sine and cosine signal (phase shift 90°) forming the components of a quadrature demodulator, capable of measuring both the amplitude and the phase of the signal of interest. In principle it is possible to multiply the signal of interest with any frequency, resulting in a heterodyne operation. However the objective of the lock-in amplifier is to shift the signal as close as possible to DC, therefore the frequency of the reference and the signal is chosen similar. In literature this is called homodyne detection, synchrodyne detection, or zero-IF direct conversion.

The result of the multiplication is the signal

\[ \begin{equation}\tag{1} V_s(t)\cdot V_r(t) = V_s(t\cdot \sqrt{2}e^{-i\omega_rt}= \frac{A_s}{\sqrt{2}}e^{i[(\omega_s-\omega_r)t+\theta]} + \frac{A_s}{\sqrt{2}}e^{-i[(\omega_s+\omega_r)t+\theta]} \end{equation} \]

It consists of a slow component with frequency \(\omega_s - \omega_r\) and a fast component with frequency \(\omega_s + \omega_r\).

The demodulated signal is then low-pass filtered with an infinite impulse response (IIR) RC filter, indicated by the symbol \(\langle \cdot \rangle\). The frequency response of the filter \(F(\omega)\) will let pass the low frequencies \(F(\omega_s - \omega_r)\) while considerably attenuating the higher frequencies \(F(\omega_s + \omega_r)\). Another way to consider the low-pass filter is an averager.

\[ \begin{equation}\tag{2} X+iY = \langle V_s(t)\cdot\sqrt{2}e^{-i\omega_r t}\rangle \approx F(\omega_s-\omega_r)\frac{A_s}{\sqrt{2}}e^{i[(\omega_s-\omega_r)t+\theta]} \end{equation} \]

The result after the low-pass filter is the demodulated signal \(X+iY\), where X is the real and Y is the imaginary part of a signal depicted on the complex plane. These components are also called in-phase and quadrature components. The transformation of X and Y into the amplitude R and phase \(\theta\) information of \(V_s(t)\) can be performed with trigonometric operations.

It is interesting to note that the value of the measured signal corresponds to the RMS value of the signal, which is equivalent to \(R = A_s/\sqrt{2}\).

Most lock-in amplifiers output the values (X,Y) and (R, \(\theta\) ) encoded in a range of –10 V to +10 V of the auxiliary output signals.

Lock-in Amplifier Applications¶

Lock-in amplifiers are employed in a large variety of applications. In some cases the objective is measuring a signal with good signal-to-noise ratio, and then that signal could be measured even with large filter settings. In this context the word phase sensitive detection is appropriate. In other applications, the signal is very weak and overwhelmed by noise, which forces to measure with very narrow filters. In this context the lock-in amplifier is employed for signal recovery. Also, in another context, a signal modulated on a very high frequency (GHz or THz) that cannot be measured with standard approaches, is mixed to a lower frequency that fits into the measurement band of the lock-in amplifier.

One example for measuring a small, stationary or slowly varying signal which is completely buried in the 1/f noise, the power line noise, and slow drifts. For this purpose a weak signal is modulated to a higher frequency, away from these sources of noise. Such signal can be efficiently mixed back and measured in the baseband using a lock-in amplifier. In Figure 3 this process is depicted. Many optical applications perform the up-mixing with a chopper, an electro-optical modulator, or an acousto-optical modulator. The advantage of this procedure is that the desired signal is measured in a spectral region with comparatively little noise. This is more efficient than just low-pass filtering the DC signal.

Figure 3: Lock-in measurement of a noisy DC signal

Signal Bandwidth¶

The signal bandwidth (BW) theoretically corresponds to the highest frequency components of interest in a signal. In practical signals, the bandwidth is usually quantified by the cut-off frequency. It is the frequency at which the transfer function of a system shows 3 dB attenuation relative to DC (BW = f_cut-off = f_-3dB); that is, the signal power at f_-3dB is half the power at DC. The bandwidth, equivalent to cut-off frequency, is used in the context of dynamic behavior of a signals or separation of different signals. This is for instance the case for fast-changing amplitudes or phase values like in a PLL or in imaging applications, or when signals closely spaced in frequency need to be separated.

The noise equivalent power bandwidth (NEPBW) is also a useful figure, and it is distinct from the signal bandwidth. This unit is typically used for noise measurements: in this case one is interested in the total amount of power that passes through a low-pass filter, equivalent to the area under the solid curve in Figure 4. For practical reasons, one defines an ideal brick-wall filter that lets pass the same amount of power under the assumption that the noise has a flat (white) spectral density. This brick-wall filter has transmission 1 from DC to f_NEPBW. The orange and blue areas in Figure 4 then are exactly equal in a linear scale.

Figure 4: Signal bandwidth and noise equivalent power bandwidth

It is possible to establish a simple relation between the f_cut-off and the f_NEPBW that only depends on the slope (or roll-off) of the filter. As the filter slope actually depends on the time constant (TC) defined for the filter, it is possible to establish the relation also to the time constant. It is intuitive to understand that for higher filter orders, the f_cut-off is closer to the f_NEPBW than for smaller orders.

The time constant is a parameter used to interpret the filter response in the time domain, and relates to the time it takes to reach a defined percentage of the final value. The time constant of a low-pass filter relates to the bandwidth according to the formula

\[ \begin{equation}\tag{3} TC=\frac{FO}{2\pi f_{cut-off}} \end{equation} \]

where FO is said factor that depends on the filter slope. This factor, along with other useful conversion factors between different filter parameters, can be read from the following table.

Table 1: Summary of conversion factors for bandwidth definitions
filter order	filter roll-off	FO	f_cut-off	f_NEPBW	f_NEPBW / f_cut-off
1^st	6 dB/oct	1.0000	0.1592 / TC	0.2500 / TC	1.5708
2^nd	12 dB/oct	0.6436	0.1024 / TC	0.1250 / TC	1.2203
3^rd	18 dB/oct	0.5098	0.0811 / TC	0.0937 / TC	1.1554
4^th	24 dB/oct	0.4350	0.0692 / TC	0.0781 / TC	1.1285
5^th	30 dB/oct	0.3856	0.0614 / TC	0.0684 / TC	1.1138
6^th	36 dB/oct	0.3499	0.0557 / TC	0.0615 / TC	1.1046
7^th	42 dB/oct	0.3226	0.0513 / TC	0.0564 / TC	1.0983
8^th	48 dB/oct	0.3008	0.0479 / TC	0.0524 / TC	1.0937

Discrete-Time Filters¶

Discrete-Time RC Filter¶

There are many options how to implement digital low-pass filters. One common filter type is the exponential running average filter. Its characteristics are very close to those of an analog resistor-capacitor RC filter, which is why this filter is sometimes called a discrete-time RC filter. The exponential running average filter has the time constant \(TC = \tau_N\) as its only adjustable parameter. It operates on an input signal \(X_{in}\lbrack n, \rbrack\) defined at discrete times \(n T_s , (n+1)T_s , (n+2)T_s\), etc., spaced at the sampling time \(T_s\) . Its output \(X_{out}\lbrack n,T_s\rbrack\) can be calculated using the following recursive formula,

\[ \begin{equation}\tag{4} X_{out}[n,T_s]=e^{-T_s/\tau_n}X_{out}[n-1,T_s]+(1-e^{-T_s/\tau_N})X_{in}[n,T_s] \end{equation} \]

The response of that filter in the frequency domain is well approximated by the formula

\[ \begin{equation}\tag{5} H_1(\omega)=\frac{1}{1+i\cdot\omega\cdot\tau_n} \end{equation} \]

The exponential filter is a first-order filter. Higher-order filters can easily be implemented by cascading several filters. For instance the 4^th order filter is implemented by chaining 4 filters with the same time constant \(TC = \tau_n\) one after the other so that the output of one filter stage is the input of the next one. The transfer function of such a cascaded filter is simply the product of the transfer functions of the individual filter stages. For an n-th order filter, we therefore have

\[ \begin{equation}\tag{6} H_n(\omega)=\frac{1}{(1+i\cdot\omega\cdot\tau_n)^n} \end{equation} \]

The attenuation and phase shift of the filters can be obtained from this formula. Namely, the filter attenuation is given by the absolute value squared \(|H_n(\omega)|^2\). The filter transmission phase is given by the complex argument \(arg\lbrack H_n(\omega)\rbrack\).

Filter Settling Time¶

The low-pass filters after the demodulator cause a delay to measured signals depending on the filter order and time constant \(TC = \tau_n\). After a change in the signal, it will therefore take some time before the lock-in output reaches the correct measurement value. This is depicted in Figure 5 where the response of cascaded filters to a step input signal is shown.

Figure 5: Time-domain step response of the demodulator low-pass filter for orders from 1 to 8.

More quantitative information on the settling time can be obtained from Table 2. In this table, you find settling times in units of the 1st-order filter's time constant (\(TC\)) for all filter orders available with the UHF Lock-in Amplifier. The values tell the time you need to wait for the filtered demodulator signal to reach 50%, 63%, 95% and 99% of the final value. This can help in making a quantitatively correct choice of filter parameters for example in a measurement involving a parameter sweep.

Table 2: Summary of Filter Settling Times
Filter order	50%	63% (1-1/e)	90%	95%	99%
1^st	0.7 · TC	1.0 · TC	2.3 · TC	3.0 · TC	4.6 · TC
2^nd	1.7 · TC	2.1 · TC	3.9 · TC	4.7 · TC	6.6 · TC
3^rd	2.7 · TC	3.3 · TC	5.3 · TC	6.3 · TC	8.4 · TC
4^th	3.7 · TC	4.4 · TC	6.7 · TC	7.8 · TC	10.0 · TC
5^th	4.7 · TC	5.4 · TC	8.0 · TC	9.2 · TC	11.6 · TC
6^th	5.7 · TC	6.5 · TC	9.3 · TC	10.5 · TC	13.1 · TC
7^th	6.7 · TC	7.6 · TC	10.5 · TC	11.8 · TC	14.6 · TC
8^th	7.7 · TC	8.6 · TC	11.8 · TC	13.1 · TC	16.0 · TC

Full Range Sensitivity¶

The sensitivity of the lock-in amplifier is the RMS value of an input sine that is demodulated and results in a full scale analog output. Traditionally the X, Y, or R components are mapped onto the 10 V full scale analog output. In such a case, the overall gain from input to output of the lock-in amplifier is composed of the input and output amplifier stages. Many lock-in amplifiers specify a sensitivity between 1 nV and 1 V. In other words the instrument permits an input signal between 1 nV and 1 V to be amplified to the 10 V full range output.

Figure 6: Sensitivity from signal input to signal output

In analog lock-in amplifiers the sensitivity is simple to understand. It is the sum of the analog amplification stages between in the input and the output of the instrument: in particular the input amplifier and the output amplifier.

In digital lock-in amplifiers the sensitivity less straightforward to understand. Analog-to-digital converters (ADC) operate with a fixed input range (e.g. 1 V) and thus require a variable-gain amplifier to amplify the input signal to the range given by the ADC. This variable-gain amplifier must be in the analog domain and its capability determines the minimum input range of the instrument. A practical analog input amplifier provides a factor 1000 amplification, thus 1 V divided by 1000 is the minimum input range of the instrument.

The input range is the maximum signal amplitude that is permitted for a given range setting. The signal is internally amplified with the suited factor, e.g. (1 mV)·1000 to result in a full swing signal at the ADC. For signals larger than the range, the ADC saturates and the signal is distorted – the measurement result becomes useless. Thus the signal should never exceed the range setting.

But the input range is not the same as the sensitivity. In digital lock-in amplifiers the sensitivity is only determined by the output amplifier, which is an entirely digital signal processing unit which performs a numerical multiplication of the demodulator output with the scaling factor. The digital output of this unit is then fed to the output digital-to-analog converter (DAC) with a fixed range of 10 V. It is this scaling factor that can be retrofitted to specify a sensitivity as known from the analog lock-in amplifiers. A large scaling factor, and thus a high sensitivity, comes at a relatively small expense for digital amplification.

One interesting aspect of digital lock-in amplifiers is the connection between input resolution and sensitivity. As the ADC operates with a finite resolution, for instance 14 bits, the minimum signal that can be detected and digitized is for instance 1 mV divided by the resolution of the ADC. With 14 bits the minimum level that can be digitized would be 122 nV. How is it possible to reach 1 nV sensitivity without using a 21 bit analog-to-digital converter? In a world without noise it is not possible. Inversely, thanks to noise and current digital technology it is possible to achieve a sensitivity even below 1 nV.

Most sources of broadband noise, including the input amplifier, can be considered as Gaussian noise sources. Gaussian noise is equally distributed in a signal, and thus generates equally distributed disturbances. The noise itself can be filtered by the lock-in amplifier down to a level where it does not impact the measurement. Still, in the interplay with the signal, the noise does have an effect on the measurement. The input of the ADC is the sum of the noise and the signal amplitude. Every now and then, the signal amplitude on top of the large noise will be able to toggle the least significant bits even for very small signals, as low as 1 nV and below. The resulting digital signal has a component at the signal frequency and can be detected by the lock-in amplifier.

There is a similar example from biology. Rod cells in the human eye permit humans to see in very low light conditions. The sensitivity of rod cells in the human eye is as low as a single photon. This sensitivity is achieved in low light conditions by a sort of pre-charging of the cell to be sensitive to the single photon that triggers the cell to fire an impulse. In a condition with more surround light, rod cells are less sensitive and need more photons to fire.

To summarize, in digital lock-in amplifiers the full range sensitivity is only determined by the scaling factor capability of the digital output amplifier. As the scaling can be arbitrary big, 1 nV minimum full range sensitivity is achievable without a problem. Further, digital lock-in amplifiers exploit the input noise to heavily increase the sensitivity without impacting the accuracy of the measurement.

Sinc Filtering¶

As explained in Principles of Lock-in Detection, the demodulated signal in an ideal lock-in amplifier has a signal component at DC and a spurious component at twice the demodulation frequency. The components at twice the demodulation frequency (called the 2ω component) is effectively removed by regular low-pass filtering. By selecting filters with small bandwidth and faster roll-offs, the 2ω component can easily be attenuated by 100 dB or more. The problem arises at low demodulation frequencies, because this forces the user to select long integration times (e.g. >60 ms for a demodulation frequency of 20 Hz) in order to achieve the same level of 2ω attenuation.

In practice, the lock-in amplifier will modulate DC offsets and non-linearities at the signal input with the demodulation frequency, resulting in a signal at the demodulation frequency (called ω component). This component is also effectively removed by the regular low-pass filters at frequencies higher than 1 kHz.

At low demodulation frequencies, and especially for applications with demodulation frequencies close to the filter bandwidth, the ω and 2ω components can affect the measurement result. Sinc filtering allows for strong attenuation of the ω and 2ω components. Technically the sinc filter is a comb filter with notches at integer multiples of the demodulation frequency (ω, 2ω, 3ω, etc.). It removes the ω component with a suppression factor of around 80 dB. The amount of 2ω component that gets removed depends on the input signal. It can vary from entirely (e.g. 80 dB) to slightly (e.g. 5 dB). This variation is not due to the sinc filter performance but depends on the bandwidth of the input signal.

Figure 7: Effect of sinc filtering

Table 3: Artifacts in the demodulation signal
Input signal	Demodulation result before low-pass filter	Result
Signal at ω	DC component	Amplitude and phase information (wanted signal)
Signal at ω		2ω component	Unwanted component (can additionally be attenuated by sinc filter)
DC offset	ω component	Unwanted component (can additionally be attenuated by sinc filter)

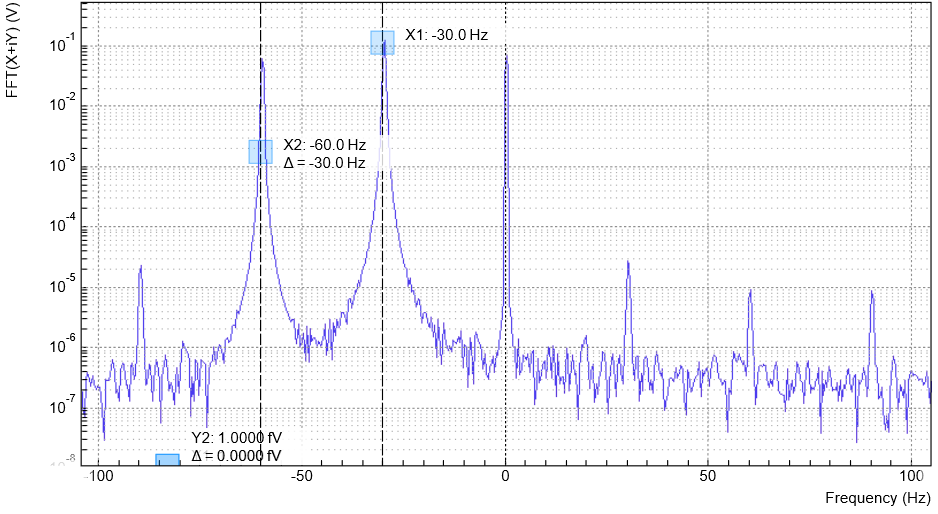
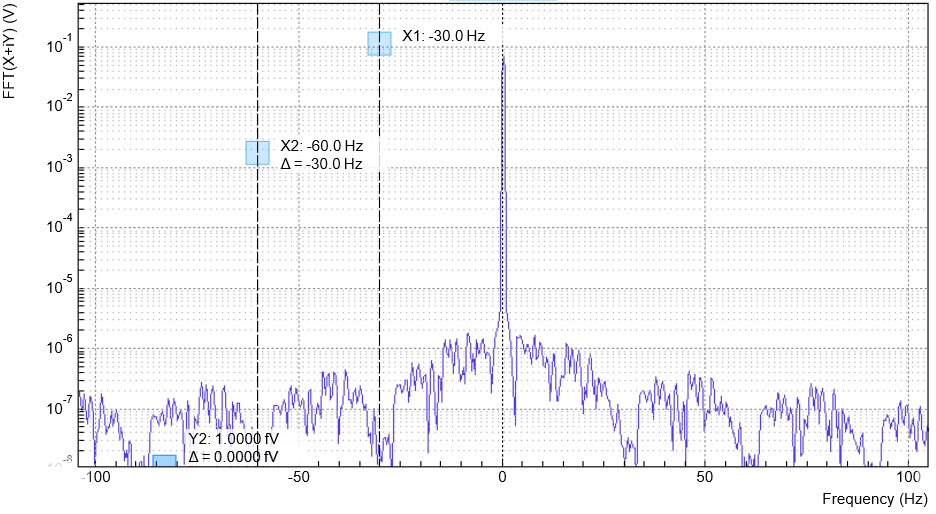
We can observe the effect of the sinc filter by using the Spectrum Analyzer Tool of the UHF Lock-in Amplifier. As an example, consider a 30 Hz signal with an amplitude of 0.1 V that demodulated using a filter bandwidth of 100 Hz and a filter order 8. In addition 0.1 V offset is added to the signal so that we get a significant ω component.

Figure 8 shows a spectrum with the sinc filter disabled, whereas for Figure 9 the sinc filter is enabled. The comparison of the two clearly shows how the sinc options dampens both the ω and 2ω components by about 100 dB.

Figure 8: Spectrum of a demodulated 30 Hz signal without sinc filter

Figure 9: Spectrum of a demodulated 30 Hz signal with sinc filter

Note

In order to put the notches of the digital filter to ω and 2ω, the sampling rate of the filter would have to be precisely adjusted to the signal frequency. As this is technically not feasible, the generated signal frequency is adjusted instead by a very small amount.

Zoom FFT¶

The concept of zoom FFT allows the user to analyze the spectrum of the input signal around a particular frequency by zooming in on a narrow frequency portion of the spectrum. This is done by performing a Fourier transform of the demodulated in-phase and quadrature (X and Y) components or more precisely, on the complex quantity X+iY, where i is the imaginary unit. In the LabOne user interface, this functionality is available in the Spectrum tab.

In normal FFT, the sampling rate determines the frequency span and the total acquisition time determines the frequency resolution. Having a large span and a fine resolution at the same time then requires long acquisition times at high sample rates. This means that a lot of data needs to be acquired, stored, and processed, only to retain a small portion of the spectrum and discard most of it in the end. In zoom FFT, the lock-in demodulation is used to down-shift the signal frequency, thereby allowing one to use both a much lower sampling rate and sample number to achieve the same frequency resolution. Typically, to achieve a 1 Hz frequency resolution at 1 MHz, FFT would require to collect and process approximately 10⁶ points, while zoom FFT only processes 10³ points. (Of course the high rate sampling is done by the lock-in during the demodulation stage, so the zoom FFT still needs to implicitly rely on a fast ADC.)

In order to illustrate why this is so and what benefits this measurement tool brings to the user, it is useful to remind that at the end of the demodulation of the input signal \(V_s(t)=A_s cos(\omega_s t+\tau)\), the output signal is \(X+iY=F(\omega_s-\omega_r)(A_s/\sqrt{2})e^{i\lbrack (\omega_s-\omega_r)t + \tau\rbrack}\) where F(ω) is the frequency response of the filters.

Since the demodulated signal has only one component at frequency ω_s–ω_r, its power spectrum (Fourier transform modulus squared) has a peak of height \((|A_s|^2/2)\cdot|F(\omega_s-\omega_r)|^2\) at ω_s–ω_r: this tells us the spectral power distribution of the input signal at frequencies close to ω_r within the demodulation bandwidth set by the filters F(ω).

Note that:

the ability of distinguish between positive and negative frequencies works only if the Fourier transform is done on X+iY. Had we taken X for instance, the positive and negative frequencies of its power spectrum would be equal. The symmetry relation G(–ω)=G*(ω) holds for the Fourier transform G(ω) of a real function g(t) and two identical peaks would appear at ±|ω_s–ω_r|.
one can extract the amplitude of the input signal by diving the power spectrum by |F(ω)|², the operation being limited by the numerical precision. This is implemented in LabOne and is activated by the Filter Compensation button: with the Filter Compensation enabled, the background noise appears white; without it, the effect of the filter roll-off becomes apparent.

The case of an input signal containing a single frequency component can be generalized to the case of multiple frequencies. In that case the power spectrum would display all the frequency components weighted by the filter transfer function, or normalized if the Filter Compensation is enabled.

When dealing with discrete-time signal processing, one has to be careful about aliasing which occurs when the signal frequencies higher than the sampling rate ω are not sufficiently suppressed. Remember that ω is the user settable readout rate, not the 2 GSa/s sampling rate of the GHFLI input. Since the discrete-time Fourier transform extends between –ω/2 and +ω/2, the user has to make sure that at ±ω/2 the filters provide the desired attenuation: this can be done either by increasing the sampling rate or resolving to measure a smaller frequency spectrum (i.e. with a smaller filter bandwidth).

Similarly to the continuous case, in which the acquisition time determines the maximum frequency resolution (\(2 \pi/T\) if T is the acquisition time), the resolution of the zoom FFT can be increased by increasing the number of recorded data points. If N data points are collected at a sampling rate ω, the discrete Fourier transform has a frequency resolution of ω/N.