Phase-locked Loop¶

Note

This tutorial is applicable to MF Instruments with the MF-PID Quad PID/PLL Controller option installed.

Goals and Requirements¶

This tutorial explains how to track the resonance frequency shift of a resonator using a phase-locked loop (PLL). To follow this tutorial, one needs to connect a resonator between Signal Output 1 and Signal Input 1.

Preparation¶

Connect the cables as shown in the figure below. Make sure that the MF Instrument is powered on and connected by USB to your host computer or by Ethernet to your local area network (LAN) where the host computer resides. After starting LabOne the default web browser opens with the LabOne graphical user interface.

Figure 1: PLL connection with MF Instrument

The tutorial can be started with the default instrument configuration (e.g. after a power cycle) and the default user interface settings (e.g. as is after pressing F5 in the browser).

Determine the Resonance of the Quartz¶

In this section you will learn first how to find the resonance of your resonator with the Sweeper Tab tool. In the Sweeper tab, one can start by defining a frequency sweep across the full instrument bandwidth and narrow down the range using multiple sweeps in order to find the resonance peak of interest. In our case, we know already that the resonance lies at around 1.8 MHz which saves us some time in finding the peak, knowing that its Q factor is rather high. The Sweeper tab and Lock-in tab settings are shown in the table below.

Note

The table below applies to instruments without the MF-MD Multi-demodulator option installed. With the option installed, the output amplitude needs to be configured in the Output Amplitudes section of the Lock-in tab.

Table 1: Settings: sweep the measurement frequency
Tab	Sub-tab	Section	#	Label	Setting / Value / State
Lock-in	All	Signal Outputs	1	Amp (V)	100.0 m / ON
Lock-in	All	Signal Outputs	1	Output 1	ON
Lock-in	All	Signal Inputs	1	50 Ω	ON
Lock-in	All	Signal Inputs	1	Diff	OFF
Lock-in	All	Demodulators	1	Osc	1
Lock-in	All	Demodulators	1	Input	Sig In 1
Lock-in	All	Data Transfer	1	Enable	ON
Sweeper	Control	Horizontal		Sweep Param.	Osc 1 Frequency
Sweeper	Control	Vertical Axis Groups		Signal Type / Channel	Demod Θ / 1
Sweeper	Control	Vertical Axis Groups		Add Signal	click
Sweeper	Control	Vertical Axis Groups		Signal Type / Channel	Demod R / 1
Sweeper	Control	Vertical Axis Groups		Add Signal	click
Sweeper	Control	Horizontal		Start (Hz)	1 M
Sweeper	Control	Horizontal		Stop (Hz)	3 M
Sweeper	History			Length	2
Sweeper	Control	Settings		Dual Plot	ON
Sweeper	Control	Settings		Run/Stop	ON

We use demodulator 1 to generate the sweep signal and to demodulate the signal transmitted through the resonator. The Lock-in settings ensure that the oscillator used both for the generation and the measurement is the same (oscillator 1). In addition, the input must be set to Signal Input 1 in accordance with the connection diagram.

Once the Sweeper button is clicked, the Sweeper will repeatedly sweep the frequency response of the quartz oscillator. The History Length of 2 allows you to keep one previous sweep on the screen while adjusting the sweep range. You can use the zoom tools to get a higher resolution on the resonance peak. To redefine the start and stop frequencies for a finer sweeper range, just click the button. This will automatically paste the plot frequency range into the Start and Stop fields of the Sweeper frequency range.

Note

The sweep frequency resolution will get finer when zooming in horizontally using the button even without changing the number of points.

When a resonance peak has been found, you should get a measurement similar to the solid lines in the two figures below. The resonance fitting tool allows us to easily determine resonance parameters such as Q factor, center frequency, or peak amplitude. To use the tool, place the two X cursors to the left and right of the resonance, open the Math sub-tab of the Sweeper tab, select "Resonance" from the left drop-down menu, and click on . Repeat this operation, once with the demodulator amplitude as the active trace in the plot, and once with the demodulator phase (see Vertical Axis Groups). The tool will perform a least-squares fit to the response function of an LCR circuit. In the limit of large Q factors, this corresponds to a fit to the square root of a Lorentzian function for the amplitude, and to an inverse tangent for the phase. The exact fitting functions are documented in the section called "Cursors and Math".

The fitting curves are added as dashed lines to the plot as shown in Figure 2 and Figure Figure 3. Since the two fits are independent, they may lead to different results if the resonance significantly deviates from a simple LCR circuit model, which often is the case if there is capacitive coupling between the leads. In this case, the fit to the phase curve which is clearly better than that to the amplitude curve yields a Q factor of about 12,800, and a center frequency of 1.8428 MHz.

The phase in Figure 3 follows a typical resonator response going from +90° to –90° when passing through the resonance on a 50 Ω input. Directly at the resonance, the measured phase is close to 0°. We will use this value as a phase setpoint for the PLL. After having completed the Sweeper measurements, turn off sweeping by clicking on . This will release the oscillator frequency from the control by the Sweeper.

Figure 2: Amplitude of the resonator’s frequency response measured with the LabOne Sweeper. Solid line are measurement data, dashed line is a fit to the response function of an LCR circuit model using the resonance fitting tool.

Figure 3: Phase of the resonator’s frequency response measured with the LabOne Sweeper. Solid line are measurement data, dashed line is a fit to the response function of an LCR circuit model using the resonance fitting tool.

Resonance Tracking with the PLL¶

Now we know the resonance frequency and the phase measured at this frequency. We can track the drift in resonance frequency by locking on to this phase, hence the name phase-locked loop (PLL). The phase-locked loop is available in the PLL tab. There are four PID (proportional-integral-derivative) controllers in each MFLI instrument, and the first two have dual use as PLL controllers. For this tutorial, we will use PLL 1. We first set up the basic PLL 1 fields as shown in the table below, using the values from the previous measurement.

Table 2: Settings: set up the phase-locked loo
Tab	Sub-tab	Section	#	Label	Setting / Value / State
PLL	PLL		1	Mode	PLL
PLL	PLL		1	Auto Mode	PID Coeff
PLL	PLL	Input	1	Setpoint (deg)	0.0
PLL	PLL	Output	1	Output	Oscillator Frequency / 1
PLL	PLL	Output	1	Center Freq (Hz)	1.8428 M
PLL	PLL	Output	1	Lower / Upper Limit (Hz)	–10k / +10 k

The upper and lower frequency (or range) relative to the Center Frequency should be chosen narrow enough so that the phase of the device follows a monotonous curve with a single crossing at the setpoint, else the feedback controller will fail to lock correctly. We select the 1^st oscillator and demodulator 1 for the phase-locked loop operation. 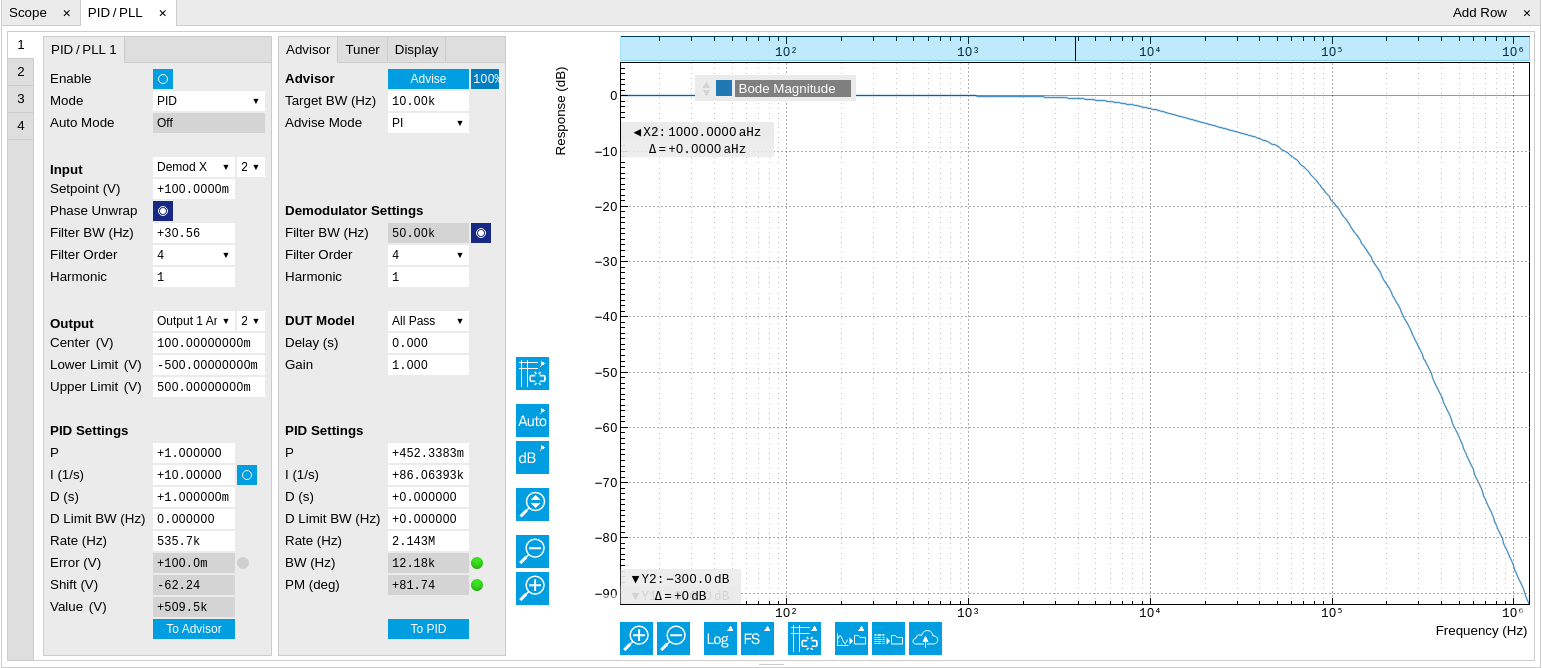Now, we need to find suitable feedback gain parameters (P, I, D) which we do using the Advisor. Set the DUT Model to Resonator Frequency, the Target BW (Hz) to 1.0 kHz, and click on to copy the Center Frequency to the resonance frequency field of the Advisor. The target bandwidth should be at least as large as the expected bandwidth of the frequency variations. In the present case, the resonator frequency is practically stable, so 1 kHz bandwidth is largely enough. Click on the button to have the Advisor find a set of feedback gain parameters using a numerical optimization algorithm. Figure 4 shows a typical view of the PLL tab after the Advisor has finished. The Advisor tries to match or exceed the target bandwidth in its simulation. The achieved bandwidth can be read from the BW (Hz) field, or directly from the 3 dB point of the simulated Bode plot on the right. The Phase Margin value of the simulation is displayed in the PM (deg) field and should exceed 45° to ensure stable feedback operation without oscillations. Once you are satisfied with the Advisor results, click on the button to transfer the feedback gain parameters to the physical PLL controller. To start PLL operation, click on the Enable button at the top of the PLL tab.

Table 3: Settings: set up and run the PID Advisor
Tab	Sub-tab	Section	#	Label	Setting / Value / State
PLL	Advisor	Advisor	1	Target BW (Hz)	1 k
PLL	Advisor	DUT Model	1	DUT Model	Resonator Frequency
PLL	Advisor	DUT Model	1	Res Frequency (Hz)	1.8 M
PLL	Advisor	DUT Model	1	Q	12.8 k
PLL	Advisor	Advisor	1	Advise	click

Figure 4: Settings and Advisor simulation in the PLL tab (typical – parameters may differ from the example)

When the PLL is locked, the green indicator next to the label Error/PLL Lock will be switched on. The actual frequency shift is shown in the field Freq Shift (Hz).

Note

At this point, it is recommended to adjust the signal input range by clicking the Auto Range button in the Lock-in tab. This often increases the signal-to-noise ratio which helps the PLL to lock to an input signal.

The easiest way to visualize the frequency drift is to use the Plotter tool. The frequency can be added to the display by using the Tree Selector to navigate to Demodulator 1 → Sample and selecting Frequency. The frequency noise increases with the PLL bandwidth, so for optimum noise performance the bandwidth should not be higher than what is required by the experiment. The frequency noise also scales inversely with the drive amplitude of the resonator.