Automatic Gain Control¶
Note
This tutorial is applicable to MF Instruments with the MF-PID Quad PID/PLL Controller option installed.
Goals and Requirements¶
This tutorial explains how to set up a PID controller for automatic gain control. We use the PID Advisor to simulate the step response of a feedback loop and the Data Acquisition tool to capture the physical step response of the loop. We perform the test using a quartz resonator between Signal Output 1 and Signal Input 1.
Preparation¶
Connect the cables as illustrated below. Make sure the MF Instrument is powered on, and then connect the MF Instrument through the USB to your PC, or to your local area network (LAN) where the host computer resides. After starting LabOne the default web browser opens with the LabOne graphical user interface.
The tutorial can be started with the default instrument configuration (e.g. after a power cycle) and the default user interface settings (e.g. as is after pressing F5 in the browser).
Automatic Gain Control¶
In this section you will learn how to control the output amplitude of your device under test with a PID controller. We will use a quartz resonator driven at its resonance frequency by the signal generator of the instrument, and measured with a demodulator.
If you are continuing from the Phase-locked Loop, then you can just leave the PLL enabled. Otherwise, you should know how to generate an excitation signal at the required frequency and how to measure the signal amplitude that you want to control. The device-under-test does not need to be a resonator.
As shown in the frequency response curve below, we are measuring an amplitude of about 4.0 mV at the peak of the resonance while driving with 100 mVpk. The goal is to have this amplitude programmable by the user on the fly.
For setting up automatic gain control, open the PID / PLL tab in which the four available PID controllers are represented in different side-tabs. Since the first two controllers have a dual use as PLLs, we’ll use PID 3 for this tutorial. We’ll define the Input of the controller as the measured lock-in R signal, and the Output as the drive amplitude. The settings are shown in the table below.
Note
The table below applies to instruments without the MF-MD Multi-demodulator option installed. With the option installed, the Output 1 Amplitude channel needs to be set to the number of the demodulator used to generate the signal in the Output Amplitudes section of the Lock-in tab.
| Tab | Sub-tab | Section | # | Label | Setting / Value / State |
|---|---|---|---|---|---|
| PID / PLL | PID / PLL | 3 | Mode | PID | |
| PID / PLL | PID / PLL | Input | 3 | Demod R / 1 | |
| PID / PLL | PID / PLL | Input | 3 | Setpoint (V) | 10 m |
| PID / PLL | PID / PLL | Output | 3 | Output 1 Amplitude / 1 | |
| PID / PLL | PID / PLL | Output | 3 | Center (V) | 0.5 |
| PID / PLL | PID / PLL | Output | 3 | Lower/Upper Limit (V) | –0.5/+0.5 |
| PID / PLL | PID / PLL | Output | 3 | Range | 0.5 |
The next step is to select the proper feedback gain parameters (P, I, D). On the MF instrument we can do this with the help of the PID Advisor. Based on a set of mathematical models for the device under test (DUT), it can simulate the step response for a certain set of feedback gain values. The PID Advisor numerically optimizes the feedback gain parameters to obtain a step response that matches or exceeds a user-specified target bandwidth.
The list of available DUT models is found in PID / PLL Tab. In case your DUT is not well described by one of the models, the methods presented here are nonetheless useful to implement certain heuristic tuning method such as the Good Gain method (Finn Haugen, Telemark University College, Norway, 2010), as they enable measurement of the closed-loop step response.
The PID Advisor offers an efficient graphical tool for setting the
feedback gain parameters manually. To access it, enable the Advanced
Mode in the Display sub-tab and select PID from the Transfer Function
menu. Three cursor lines will be added to the display section which
represent the frequency dependence of the P, I, and D part of the PID
controller transfer function. The cursors can be dragged, allowing you
to define a target Bode plot. If you enable the Advisor Link button
,
the feedback gain parameters derived from the cursors are linked with
the simulation parameters from the Advisor from where they can be
transferred to the instrument.
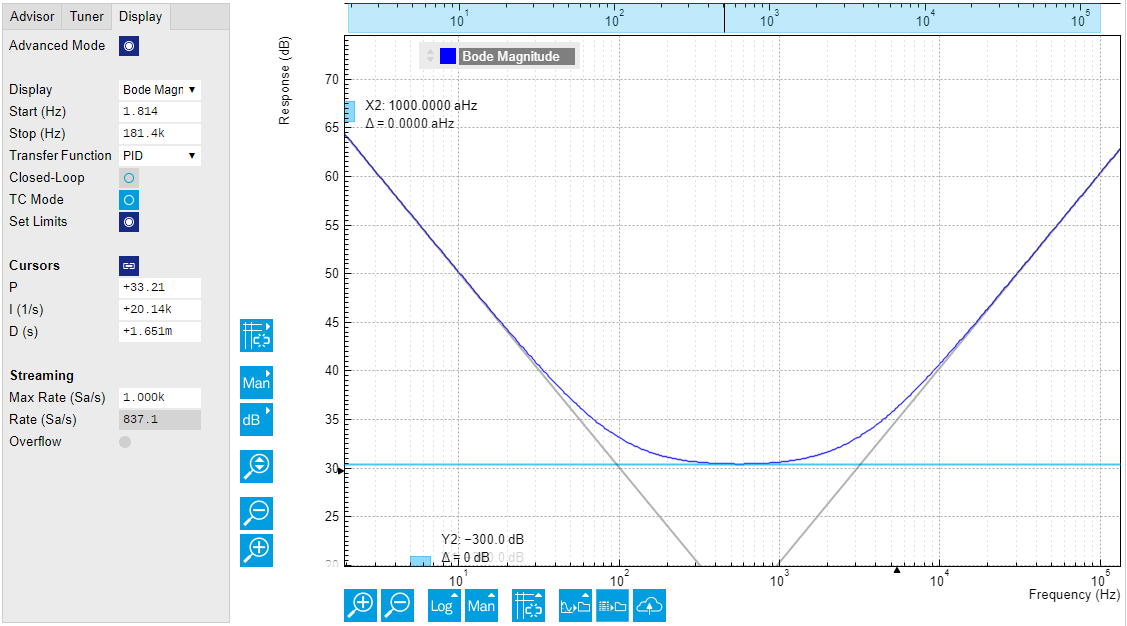
Simulating the Device Under Test¶
In the Advisor sub-tab, select "Resonator Amplitude" as the model of the DUT. This model is characterized by four parameters: delay, gain, center frequency, and Q. The latter two can easily be determined from a frequency response measurement in the Sweeper tab using the resonance fitting tool available in the Math sub-tab as described in Determine the Resonance of the Quartz. We obtain a Q factor of \~12,800 and a center frequency of 1.8428 MHz. The delay value represents extra delays such as those coming from cables (typically 4 to 5 ns per meter). Since we use short cables these are negligible and we can leave the delay parameter at 0 s. The gain value parametrizes overall signal gain or attenuation between PID controller output and input, including unit conversion. In our case, measuring an R amplitude of 4.0 mVrms on resonance while the drive amplitude is set to 100 mVpk, we have a gain of 0.040.
With the Mode selector in the Advisor sub-tab, you can define which of the feedback gain parameters the Advisor uses for his optimization. E.g., when you select PI advise mode, P and I parameters are varied but D is fixed at the value presently set. In this way you can choose the most efficient way of using the Advisor: you can have everything be done by the Advisor, you can control some of the parameters manually and have the Advisor deal with the rest, or you do all the adjustments manually and use the Advisor only to simulate the outcome.
We leave the D parameter at 0 and let the Advisor run in PI mode. Enter
a target BW of 1 kHz and click on the 
button. The Advisor will suggest some values for P and I. The BW field
indicates the bandwidth of the simulated loop, with a green lamp showing
that the target bandwidth was reached or exceeded. The PM field shows
the phase margin, with a green lamp indicating a stable feedback loop.
In the given example, the resonator has a bandwidth of about 140 Hz, so the target bandwidth of 1 kHz is just about within reach. However, in order to reach this value, the corresponding demodulator filter bandwidth may need adjustment. It should be larger than the target bandwidth, but not larger than necessary in order to avoid excessive noise. When enabling Auto Bandwidth (the checkbox next to the Filter BW field in the Demodulator Settings), the PID Advisor selects a suitable demodulator bandwidth which later will be transferred automatically to the demodulator.
The Bode plot on the right-hand side of the tab corresponds to the simulated closed-loop frequency response based on the P, I, and D gain values and the DUT model presently set in the Advisor sub-tab. In order to show the simulated closed-loop step response for our example as in Figure 4, set Display to Step Response in the Display sub-tab.
Note
In case a demodulator measurement is selected as the PID input, the Advisor will control the corresponding demodulator filter bandwidth, but not the filter order. If you encounter problems with oscillating feedback, bear in mind that low-order filters often lead to more stable feedback loop behavior because of their smaller delay.
| Tab | Sub-tab | Section | # | Label | Setting / Value / State |
|---|---|---|---|---|---|
| PID / PLL | Advisor | Advisor | 3 | Target BW (Hz) | 1 k |
| PID / PLL | Advisor | Advisor | 3 | Advise Mode | PI |
| PID / PLL | Advisor | Demodulator Settings | 3 | Filter BW / Auto Bandwidth | ON |
| PID / PLL | Advisor | DUT Model | 3 | DUT Model | Resonator Amplitude |
| PID / PLL | Advisor | DUT Model | 3 | Delay | 0.0 s |
| PID / PLL | Advisor | DUT Model | 3 | Gain | 0.040 |
| PID / PLL | Advisor | DUT Model | 3 | Center Frequency | 1.8 M |
| PID / PLL | Advisor | DUT Model | 3 | Q | 12.8 k |
| PID / PLL | Display | 3 | Display | Step Response | |
| PID / PLL | Advisor | Advisor | 3 | Advise | ON |
Measuring the Step Response¶
Once you are satisfied with the Advisor results, click on the 
button to transfer the feedback gain parameters to the physical PID /
PLL controller represented on the left. Enable the PID / PLL controller
and check, e.g. using the
Plotter Tab,
whether demodulator 1 R has settled at the setpoint of 10 mV. Toggling
the setpoint in the PID / PLL tab will then immediately be visible as a
step in the Plotter. To capture the step response, the
Data Acquisition Tab
is the tool of choice. Open the DAQ tab and configure the trigger in the
Settings and Grid sub-tabs according to the table below. .Settings: set
up the Data Acquisition tool
| Tab | Sub-tab | Section | # | Label | Setting / Value / State |
| DAQ | Settings | Trigger Settings | Trigger Signal | Demod 1 R | |
| DAQ | Settings | Trigger Settings | Level (V) | 11 m | |
| DAQ | Settings | Trigger Settings | Hysteresis (V) | 0 | |
| DAQ | Settings | Horizontal | Delay (s) | –1 m | |
| DAQ | Grid | Grid Settings | Mode | Linear | |
| DAQ | Grid | Grid Settings | Duration (s) | 5 m | |
| Lock-in | All | Data Transfer | 1 | Rate (Hz) / Enable | 100 k / ON |
We also increased the demodulator data transfer rate to get a high time
resolution for this measurement. Start the Data Acquisition tool by
clicking on 
Any time you toggle the setpoint across the Trigger Level (e.g. from 10
mV to 12 mV), a single trace will be recorded and displayed in the DAQ
tab as shown in the figure below.
Comparing Figure 5 with Figure 4 demonstrates the excellent quantitative match between simulation and measurement.