HDAWG precompensation curve fit#
Demonstrate how to use the precompensation module to fit filter parameters for a measured signal.
Requirements:
LabOne Version >= 22.08
Instruments: 1 x HDAWG Instrument
[1]:
from zhinst.toolkit import Session
import numpy as np
from scipy import signal
from lmfit import Model
session = Session("localhost")
device = session.connect_device("DEVXXXX")
[2]:
sampling_rate = device.system.clocks.sampleclock.freq(2.4e9, deep=True)
Generate target signal#
[3]:
MIN_X = -96
MAX_X = 5904
x_values = np.array(range(MIN_X, MAX_X))
x_values = [element / sampling_rate for element in x_values]
target_signal = np.array(np.concatenate((np.zeros(-MIN_X), np.ones(MAX_X))))
Generate actual signal#
Generate “actual signal” through filtering the initial signal with an exponential filter and add noise.
[4]:
TAU = 100e-9
AMPL = 0.4
# calculate a and b from amplitude and tau
alpha = 1 - np.exp(-1 / (sampling_rate * TAU * (1 + AMPL)))
if AMPL >= 0.0:
k = AMPL / (1 + AMPL - alpha)
signal_a = [(1 - k + k * alpha), -(1 - k) * (1 - alpha)]
else:
k = -AMPL / (1 + AMPL) / (1 - alpha)
signal_a = [(1 + k - k * alpha), -(1 + k) * (1 - alpha)]
signal_b = [1, -(1 - alpha)]
distorted_signal = np.array(
signal.lfilter(signal_b, signal_a, target_signal)
+ 0.01 * np.random.normal(size=target_signal.size)
)
Prepare the Precompensation Advisor module#
[5]:
module = session.modules.precompensation_advisor
module.device(device)
# Manually load wave through the inputvector node.
module.wave.input.source("manual")
# Use a single exponential filter.
module.exponentials[0].enable(True)
Fitting the parameters#
[6]:
def labone_exponential_filter(module_handle, input_signal, amplitude, timeconstant):
"""Calculate precompensated signal for a single exponential filter.
Uploads the input_signal to the precompensationAdvisor module and returns
the simulated forward transformed signal with an exponential
filter(amplitude,timeconstant).
Args:
module_handle: Precompensation Advisor Module.
input_signal: Amplitude data used as a signal source.
amplitude: Amplitude of the exponential filter.
timeconstant: Time constant (tau) of the exponential filter.
"""
module_handle.exponentials[0].amplitude(amplitude)
module_handle.exponentials[0].timeconstant(timeconstant)
module_handle.wave.input.inputvector(input_signal)
return np.array(module_handle.wave.output.forwardwave()["x"])
model = Model(
labone_exponential_filter, independent_vars=["module_handle", "input_signal"]
)
result = model.fit(
target_signal,
input_signal=distorted_signal,
module_handle=module,
amplitude=0.0,
timeconstant=1e-4,
fit_kws={"epsfcn": 1e-3},
)
# 'epsfcn' is needed as filter parameters are discretized in precompensationAdvisor
# module, otherwise fitting will not converge
print(result.fit_report())
[[Model]]
Model(labone_exponential_filter)
[[Fit Statistics]]
# fitting method = leastsq
# function evals = 72
# data points = 6000
# variables = 2
chi-square = 0.30571694
reduced chi-square = 5.0970e-05
Akaike info crit = -59303.6624
Bayesian info crit = -59290.2634
[[Variables]]
amplitude: 0.39604559 +/- 0.00115905 (0.29%) (init = 0)
timeconstant: 1.0186e-07 +/- 3.8885e-10 (0.38%) (init = 0.0001)
[[Correlations]] (unreported correlations are < 0.100)
C(amplitude, timeconstant) = -0.752
Plot results#
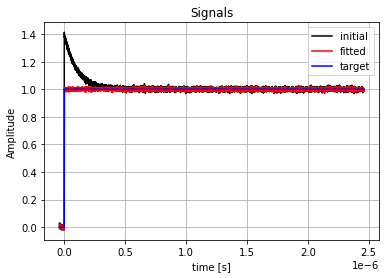
[7]:
import matplotlib.pyplot as plt
_, axis = plt.subplots()
axis.plot(x_values, result.init_fit, "k", label="initial")
axis.plot(x_values, result.best_fit, "r", label="fitted")
axis.plot(x_values, target_signal, "b", label="target")
axis.legend()
axis.ticklabel_format(axis="both", style="sci", scilimits=(-2, 2))
axis.set_xlabel("time [s]")
axis.set_ylabel("Amplitude")
plt.title('Signals')
plt.grid()
plt.show()