Basic Waveform Playback

Note

This tutorial is applicable to all SHFSG+ Instruments.

Goals and Requirements

The goal of this tutorial is to demonstrate the basic use of the

SHFSG+, by demonstrating simple waveform generation and playback. In order to visualize the multi-channel signals, an oscilloscope with sufficient bandwidth and channel number is required.

Preparation

Connect the cables as illustrated below. Make sure that the instrument is powered on and connected by Ethernet to your local area network (LAN) where the host computer resides. After starting LabOne, the default web browser opens with the LabOne graphical user interface.

Note

The instrument can also be connected via the USB interface, which can be simpler for a first test. As a final configuration for measurements, it is recommended to use the 1GbE interface, as it offers a larger data transfer bandwidth.

Figure 1: Connections for the arbitrary waveform generator basic playback tutorial

The tutorial can be started with the default instrument configuration (e.g. after a power cycle) and the default user interface settings (e.g. after pressing F5 in the browser).

Waveform Generation and Playback

In this tutorial we generate signals with the AWG and visualize them with the scope. In a first step we enable the Output of the

SHFSG+ and set the Output Range. We also set the RF center frequency to 1 GHz. In this example, we will use the RF path, which supports center frequencies in the range 0.6 - 8 GHz. When using the LF path, the center frequency can be set in the range 0 - 2 GHz. Additionally, we configure the scope with a suitable time base (e.g. 500 ns per division) and range (e.g. 0.2 V per division). The following table summarizes the necessary settings.

Table 1: Settings: enable the output

Tab	Sub-tab	Label	Setting / Value / State
Output	Signal Output 1	On	ON
Output	Signal Output 1	Range (dBm)	10
Output	Channel 1	Center Freq (Hz)	1.0 G
Output	Signal Output 1	Output Path	RF

Table 2: Settings: configure the external scope

Scope Setting	Value / State
Ch1 enable	ON
Ch1 range	0.2 V/div
Timebase	500 ns/div
Trigger source	Ch1
Trigger level	200 mV
Run / Stop	ON

Figure 2: LabOne UI: Output tab

In the Output Tab, we configure the first output channel. The final signal amplitude is determined by the dimensionless signal amplitude stored in the waveform memory scaled to the set Range in dBm of the channel. The necessary settings are summarized in the following table.

Table 3: Settings: configure the AWG output

Tab	Sub-tab	Section	#	Label	Setting / Value / State
AWG	Control			Sampling Rate	2 GHz
Digital Modulation		Modulation Control	1	Modulation	OFF
Digital Modulation		AWG Outputs		Amplitude	1.0

To operate the AWG we need to specify a sequence program through a C-type language. This program is then compiled and uploaded to the instrument where it is executed in real time. Writing the sequence program can be done interactively by typing the program in the sequence window. Let’s start by typing the following code into the sequence editor.

wave w_gauss = 1.0*gauss(8000, 4000, 1000);
playWave(1, w_gauss);

In the first line of the program, we generate a waveform with a Gaussian shape with a length of 8000 samples and store the waveform under the name w_gauss. The peak center position 4000 and the standard deviation 1000 are both defined in units of samples. You can convert them into time by dividing by the chosen Sampling Rate (2.0 GSa/s by default). The waveform generated by the gauss function has a peak amplitude of 1. This amplitude is dimensionless and the output amplitude of the physical signal is given by this number multiplied with the voltage determined by the selected output range (here we chose 0 dBm). To calculate the maximum amplitude \(V_p\) in Volts use: \(V_p=\sqrt{2 * 10^{P_\mathrm{max}/10} * 10^{-3} \,\mathrm{W} * 50\,\Omega}\), where \(P_\mathrm{max}\) is the Range setting in dBm. \(V_p\) corresponds to the peak voltage of a signal of a given power when connected to a \(50\,\Omega\) load. To calculate he RMS amplitude \(V_{rms}\), divide by \(\sqrt{2}\), i.e. \(V_{rms}=\frac{V_p}{\sqrt{2}}\). Of course, the scaling factor of 1.0 in the waveform definition can be replaced by any other value. Finally, the code line is terminated by a semicolon according to C conventions.

With the second line of the program, the generated waveform w_gauss is played on Output 1. We use the syntax playWave(1,w_gauss) to play a Gaussian signal in the real quadrature of the complex output. For a more detailed discussion of how the playWave command routes the AWG outputs to generate complex signals, see the Digital Modulation Tutorial. Note that the syntax of the playWave command and the values of other parameters, such as the waveform amplitude, can yield signals that are either below or above the maximum output power. If a signal happens to be above the maximum output power, it will clip at the DAC and may be distorted. For more details on playWave and how different amplitude settings influence the final signal, see the Modulation Tutorial.

Note

For this tutorial, we will keep the description of the Sequencer instructions short. You can find the full specification of the LabOne Sequencer language in LabOne Sequence Programming

Note

The AWG has a waveform granularity of 16 samples, and a minimum waveform length of 32 samples when using playWave commands or 16 samples when using the command table (see the Pulse-level Sequencing Tutorial ). It’s recommended to use waveform lengths that are multiples of 16, to avoid having ill-defined samples between successively played waveforms. Waveforms that are not multiple of 16 samples are automatically padded with 0s and a compiler warning is issued.

By clicking on , the sequence program is compiled into sequence instructions that are then uploaded to the device together with the waveform data. A successful upload is indicated by a green Compiler Status LED. Any error that causes an upload failure of either the sequencer instruction or waveform data is indicated by a red status light.

Note

The Advanced tab shows how the sequence instructions translate to assembly language for the onboard FPGA.

By clicking on the Waveform sub-tab, we see that our Gaussian waveform appeared in the list. The Memory Usage field at the bottom of the Waveform sub-tab shows what fraction of the instrument memory is filled by the waveform data. The Waveform Viewer sub-tab allows you to graphically display the currently marked waveform in the list.

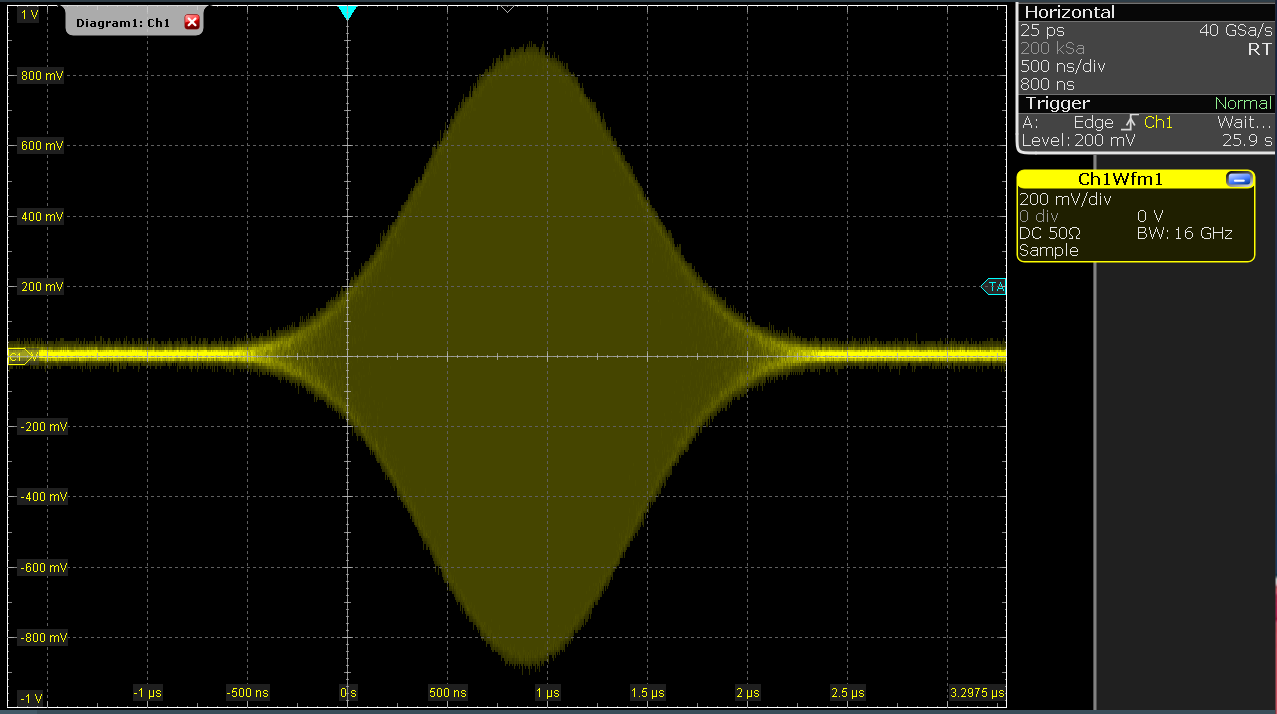
Clicking on executes the uploaded AWG program. Since we have armed the scope previously with a suitable trigger level, it has captured our Gaussian pulse with a FWHM of about 1.5 μs and a carrier frequency of 1.0 GHz, as shown in Figure Figure 3.

Figure 3: Scope shot of a Gaussian pulse generated by the AWG

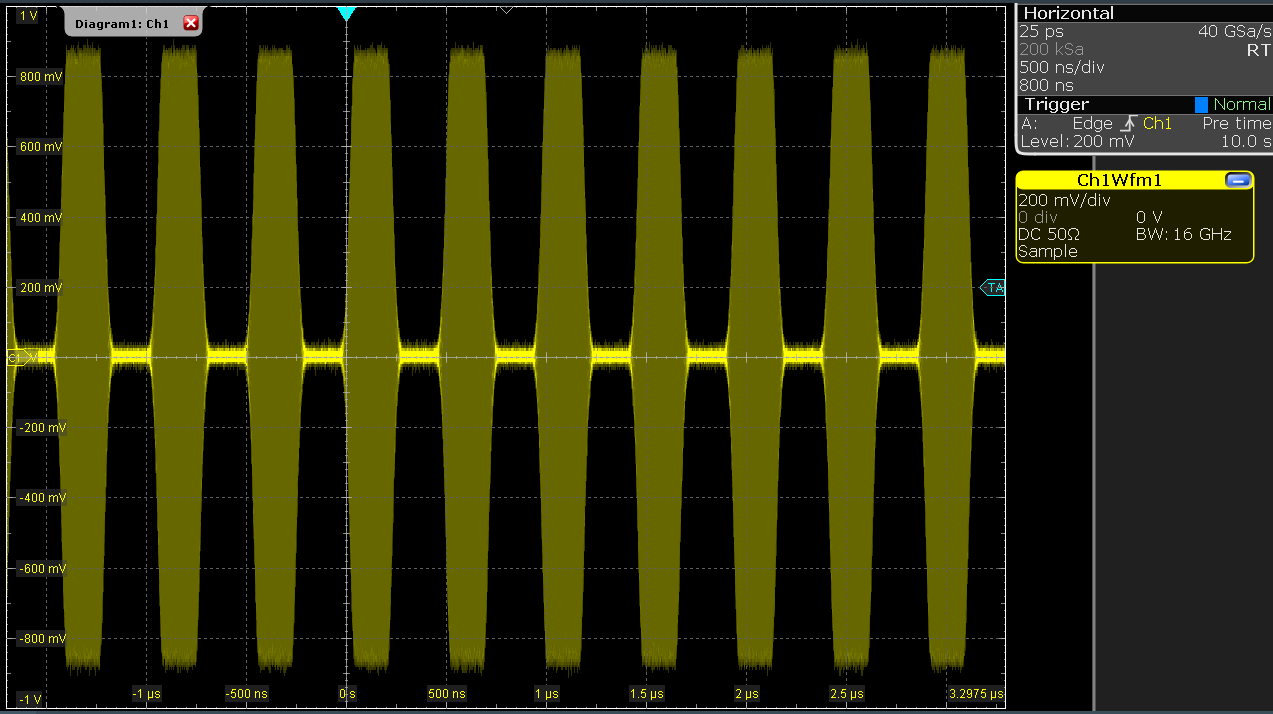
The LabOne Sequencer language offers various run-time control. An important functionality, e.g. for real-time averaging of an experiment, is the repetition of a sequence. In the following example, all the code within the curly brackets {...} is repeated 5 times. Upon clicking and , we observe 5 short Gaussian pulses in a new scope shot, see Figure 4.

wave w_gauss = 1.0 * gauss(640, 320, 50);

repeat (5) {
  playWave(1, w_gauss);
}

Figure 4: Burst of Gaussian pulses generated by the AWG and captured by the scope

In order to generate more complex waveforms, the LabOne Sequencer programming language offers a rich toolset for waveform manipulation. In addition to a selection of standard waveform generation functions, waveforms can be added, multiplied, scaled, concatenated, and truncated. It’s also possible to use compile-time evaluated loops to generate pulse series with systematic parameter variations – see LabOne Sequence Programming for more information. In the following code example, we make use of some of these tools to generate a pulse with a smooth rising edge, a flat plateau, and a smooth falling edge. We use the cut function to cut a waveform at defined sample indices, the ones function to generate a waveform with constant level 1.0 and length 320, and the join function to concatenate three (or arbitrarily many) waveforms.

wave w_gauss = gauss(640, 320, 50);
wave w_rise = cut(w_gauss, 0, 319);
wave w_fall = cut(w_gauss, 320, 639);
wave w_flat = rect(320, 1.0);

wave w_pulse = join(w_rise, w_flat, w_fall);

while (true) {
  playWave(1, w_pulse);
}

Note that we replaced the finite repetition by an infinite repetition by using a while loop. Loops can be nested in order to generate complex playback routines. The output generated by the program above is shown in Scope shot of an infinite pulse series generated by the AWG.

Figure 5: Scope shot of an infinite pulse series generated by the AWG

As programs get longer, it becomes useful to store and recall them. Clicking on allows you to store the present program under a new name. Clicking on then saves your program to the file name displayed at the top of the editor. As you begin to work on sequence programs more regularly, it’s worth using some of the editor keyboard shortcuts listed in Sequence Editor Keyboard Shortcuts.

It’s also possible to iterate over the samples of a waveform array and calculate each one of them in a loop over a compile-time variable cvar. This often allows sequences to go beyond the possibilities of using the predefined waveform generation function, particularly when using nested formulas of elementary functions like in the following example. The waveform array needs to be pre-allocated e.g. using the instruction zeros.

const N = 1024;
const width = 100;
const position = N/2;
const f_start = 0.1;
const f_stop = 0.2;
cvar i;
wave w_array = zeros(N);
for (i = 0; i < N; i++) {
  w_array[i] = sin(10/(cosh((i-position)/width)));
}

playWave(w_array);

It is also possible to use waveforms stored as a list of values in a file. If the file is stored in the location (C:\Users\<user name>\Documents\Zurich Instruments\LabOne\WebServer\awg\waves\ under Windows or ~/Zurich Instruments/LabOne/WebServer/awg/waves/ under Linux), you can then play back the wave by referring to the file name without extension in the sequence program:

playWave("wave_file");

If you prefer, you can also store it in a wave data type first and give it a new name:

wave w = "wave_file";
playWave(w);

For more information about the file format, please refer to the AWG Module Section of the LabOne Programming Manual.

Using the LF Path

The LF path bypasses the upconversion chain to allow center frequencies in the range DC to 2 GHz to be generated. The AWG sequencer can be programmed in the same way as with the RF path. The main differences is that the maximum output power of the LF path is +5 dBm (compared to +10 dBm for the RF path) and that the latency of the LF path is shorter than that of the RF path, due to the shorter analog path.

The center frequency of the LF path can be set in multiples of 100 MHz, just as with the RF path. When combined with correct usage of waitDigTrigger and resetOscPhase commands, this ensures that the initial phase of a played waveform will be reproducible within a given experimental run, as in the following example:

const length = 128;
const amp = 1;
wave = gaussian(length, amp, length/2, length/8);

while (1) {
  waitDigTrigger(1);
  resetOscPhase();
  playWave(1, 2, wave);
}